本文将由新祥旭考研邱老师对2024年华东师范大学数学专业考研进行解析。主要有以下板块:专业简介、招生人数、考试科目、参考书目、分数线、备考经验等几大方面。
一、专业简介
数学科学学院硕士研究生有基础数学、计算数学、应用数学、数学教育四个专业。基础数学专业是国家级和上海市重点学科,本专业国内外享有盛名。(1) 代数学团队学科带头人为谈胜利教授,研究方向为代数几何、表示论与数论等;(2)几何与拓扑团队学科带头人为邱瑞锋教授与刘钢教授,研究方向为低维拓扑、几何分析与黎曼几何、复几何等;(3)分析学团队学科带头人为王勤教授,研究方向为算子代数、实分析和复分析等。计算数学专业目前有专任教师8人,其中教授5人,副教授3人。学术带头人和研究团队:羊丹平教授、黎芳教授、潘建瑜教授、王元明教授、朱升峰教授、郭学萍副教授、张向韵副教授、郑海标副教授。主要特色和优势研究方向涵盖科学与工程计算的多个方向,包括微分方程数值解法、有限元方法及其应用、代数方程组预处理方法、数值最优化、图像处理、机器学习、形状与拓扑优化、数据降维、多区域多物理场建模与模拟、并行算法、计算力学、工业应用软件系统研发等。研究成果获教育部、山东省和陕西省科技进步一等奖和二等奖5项。 应用数学专业包含应用常微分方程、应用偏微分方程、运筹学与控制论研究方向。应用常微分方程、应用偏微分方程研究方向是上海市重点学科,同时加入数学物理团队,数学教育专业,数学教育团队是我校传统优秀特色团队,是国内最好的数学教育研究团队,拥有教授2人、副教授2人、副研究员1名、副编审1人、讲师3人。研究团队:范良火教授、熊斌教授、刘攀副教授、吴颖康副教授、鲁小莉副研究员、程靖讲师、何忆捷讲师、廖蔡生讲师、胡耀华副编审。创办《数学教学》、《Asian Journal for Mathematics Education》等学术杂志;2021年承办第十四届国际数学教育大会。目前团队成员中含数学教育国际顶尖期刊编委、Paul Erdos奖获得者等多名国际著名数学教育学家。
主要研究方向:
01 (全日制)基础数学
02 (全日制)计算数学
03 (全日制)应用数学
04 (全日制)数学教育
专业课程:
学位基础课:实分析与复分析I、代数学I、几何与拓扑I、概率论、科学计算、偏微分方程。其他各导师开设的专业必修课程和专业选修课程。
研究生毕业后主要去向:
硕士毕业生可以在中小学、工农业、交通运输、天文气象、航空航天、地质矿产、财政金融、保险核算等部门从事与数学相关的工作。 博士毕业生可以在高等学院校担任数学的教学与科研;在自然科学、技术科学、管理科学和工程设计等研究院所承担理论和实际课题。
二、专业目录
招生年份:2023年
拟招生人数:
全日制:128
推免上限:70
备注:数学学科按学科(不按专业)进行统一招生。应用数学研究方向大类中包含"金融数学"研究方向为与亚欧商学院合作项目,第一学期申请,该项目需另外付给外方学费
考试科目:
①101思想政治理论
②201英语(一)
③626数学分析
④817高等代数
初试范围:
626数学分析:a.实数的完备性(区间套定理、聚点定理、有限覆盖定理、柯西收敛准则、确界定理、单调有界定理);b.单变量函数(极限、连续性、导数与微分、泰勒公式(含微分中值定理)及函数的泰勒级数展开、不定积分、定积分及其应用、反常积分、周期函数的傅里叶级展开、数项级数的收敛性、函数项级数的收敛性及和函数的性质);c.多变量函数(极限与累次极限、连续性、偏导数与全微分、泰勒公式与极值问题、含参变量积分,第一、二型曲线积分,重积分(含格林公式),第一、二型曲面积分(含高斯公式与斯托克斯公式),隐函数定理及其应用。
817高等代数:多项式、 行列式、 线性方程组、矩阵、二次型、线性空间、线性变换、λ-矩阵、欧几里得空间、向量代数、若尔当典范型。
复试范围:
1.综合卷(包括抽象代数,复变函数,微分几何,常微分方程)(笔试),《近世代数》韩世安、林磊编著,科学出版社;《复变函数》钟玉泉,高等教育出版社;《微分几何》陈维恒,北京大学出版社; 《常微分方程》叶彦谦,高等教育出版
2.专业基础知识的综合能力和应用能力(口试)。
3.外语听力,口语测试(专业)。注:若由于疫情防控需要采取网络远程形式进行复试则取消笔试。
三、推荐参考书目
张天德《数学分析》
张天德《高等代数》
参考书目仅供建议,考生还需根据考试范围自行进行拓展阅读
四、2023年复试分数线
318(不接受调剂)
统考计划74
五、2023年拟录取名单


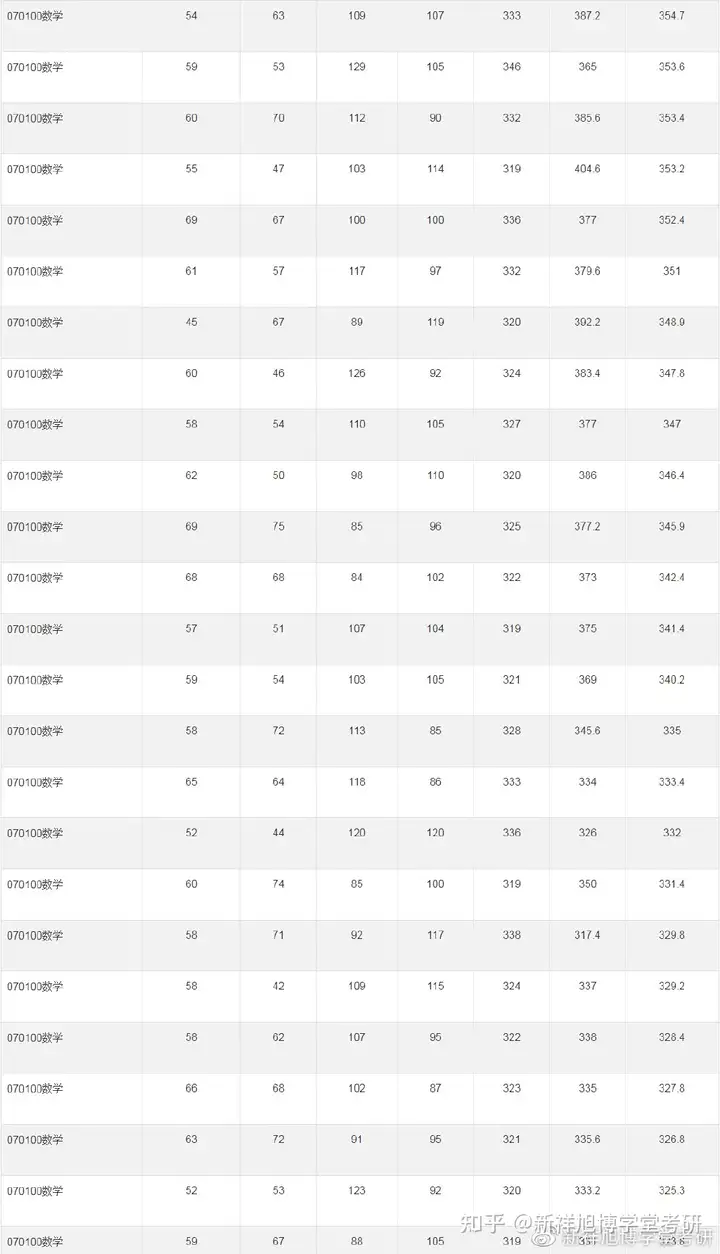
六、2022年报考录取数据
报考人数:422
录取人数:75
七、备考建议
我的数分高代课本用的是华东师大第四版的《数学分析》(已经出第五版了)和北大第四版《高等代数》。我是从四、五月抽时间开始复习,把数分高代以及书上的课后习题都过一遍,重视证明过程,同时把基础知识点都整理到笔记本上(以防后面遗忘知识点好找),后面我怕时间来不及就把数分的含参量积分以及后面的内容先跳过了,打算之后进行第二轮课本复习的时候把它补回来。七月底月开始第二轮复习,这个过程比较长,除了课本知识点的巩固,同时做裴礼文的《数学分析中的典型问题与方法》和王利广的《高等代数中的典型问题与方法》,整理总结同类型题目到错题本上,不断积累,在复习过程中遇到特别难的(第一遍只是看懂,方法过程根本想不到的那种)我都会做标记,等到第三轮强化时再看,然后过程中有遗忘的知识点就翻开之前做的笔记找,两轮结束时已经十一月了,其中我把含参量积分的理论部分跳过了,只练练了这一章的计算部分,最后看整理的笔记和错题本,同时做了几套真题,正确率我没在意,然后就上考场了。同学说华师大今年数分有几道是李傅山的《数学分析中的问题与方法》中出过的同类型题,我没来得及做,然后感觉刷题不在多,而在于精。一道题目搞清楚之后最好能举一反三。我的高代不好,因为高代题目太灵活,然后我有些地方思考的过于表面,不够深入,题目与题目之间的联系也不够密切,高代的向量代数北大课本没有,可以用谢启宏的《高等代数学》作为教材补充。数分好一些,因为我属于比较仔细的人,计算题会做了就几乎不会出现因为马虎计算失误的问题,而这次华师大去掉了判断题加大了计算题的考察也更适合我,比较幸运。
题型:判断题(今年改成填空题),计算题和证明题各五道。
判断题就是举反例,平时复习记笔记多积累:计算题知道用哪一章知识点,尽量保证正确率,或者多得点步骤分:证明题也是要结合知识点和题干,重视课本的证明过程。
时间安排:
我七月到十月是早上八点半左右开始到晚上十点,中午会午睡,最后两个月是九点多到晚上十二点,早起对我来说太难了,还是熬夜比较适合我。其他的事情尽可能自己去协调,比如入党转正以及论文等。
总结:
以上我讲的最多的就是什么适合我,什么不适合我,比如证明不好计算好,我就多写证明少做计算,记忆力不好我就多做笔记,多背几遍政治和英语模板。我觉得找到更适合自己的学习方法、节奏很重要。再就是我觉得看视频比自己看书效率高,选择适当的倍速,边听边记,一定要过脑子,遇到不会的多听几遍,一天学下来也不会太累,就是有点费耳朵,有条件的同学建议选个好耳机。
复试比不算高也不算低,进了复试只要认认真真准备就有机会上岸的。主要内容又抽象代数、复变函数、微分几何、常微分方程这几个科目。老师也都十分友好,不会问太难的题目。再提交资料是一定要做到实事求是,因为倒是很有可能在会针对这个像你进行提问,所以一定要真实,保证被问到时能说点东西,心态上要保持冷静,要有自信,尤其是在初试成绩有优势的情况下。



























